Attention Is All You Need

Paper: Attention is all you need

Authors: Vaswani et al. (2017)

The Transformer architecture revolutionized sequence-to-sequence modeling by relying entirely on attention mechanisms, dispensing with recurrence and convolutions. I've read this paper before but I think it's important to revisit the fundamentals and ask questions more deeply to clarify my doubts before revisiting and building onto subsequent related LLMs concepts on tokenisation, RLHF, PPO, Quantisation etc. for the next few days of this challenge.

This article serves to help refine my own understanding of the transformer architecture and will be updated as I review this concept again and again.

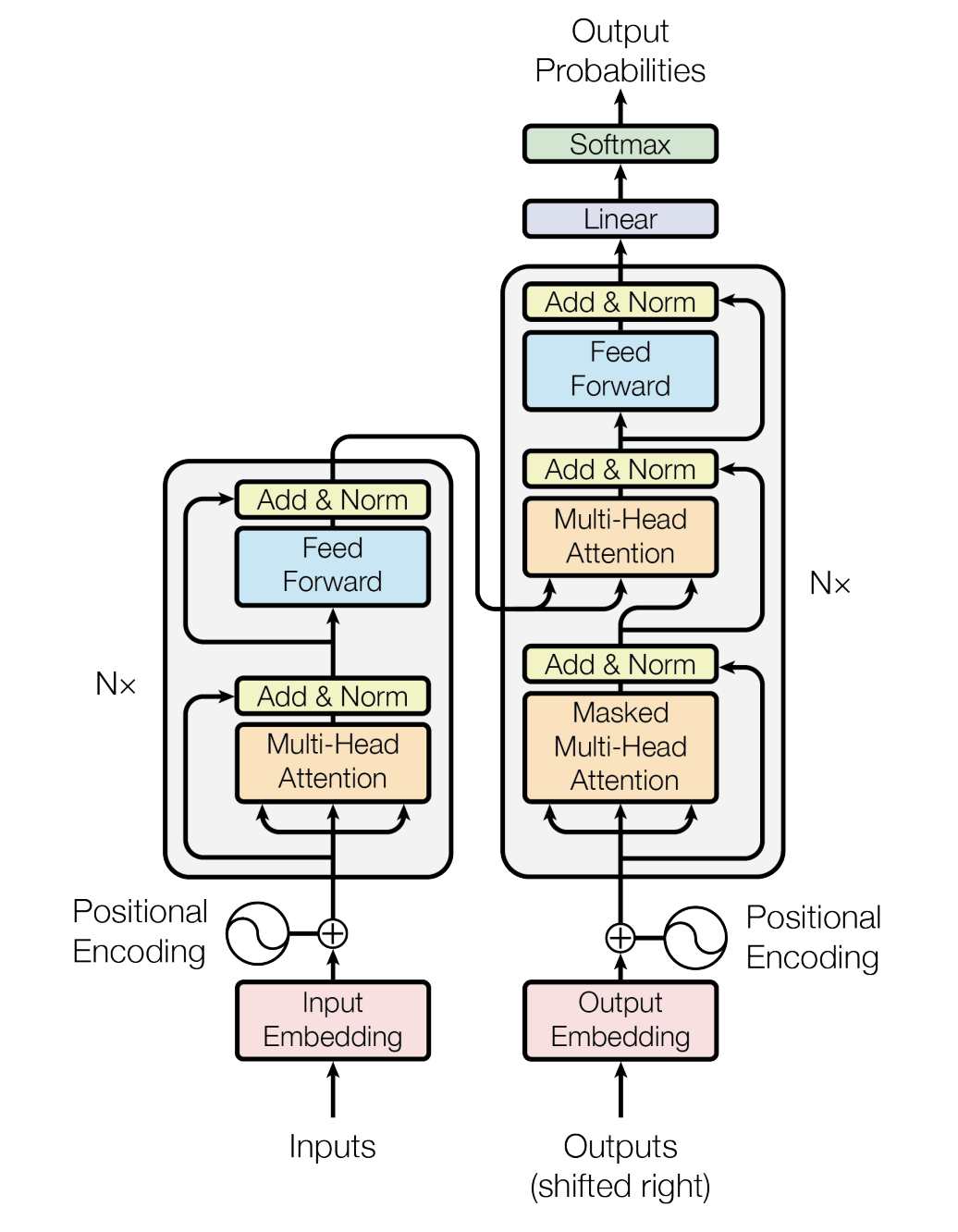
Key Components

Encoder - Decoder

The encoder takes in the input and represent it as a matrix --> Decoder will use this encoded representation and iteratively product an output.

Self-Attention Mechanism

The scaled dot-product attention is computed as:

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

Where:

• $Q$ (queries), $K$ (keys), and $V$ (values) are linear projections of the input
• $d_k$ is the dimension of the keys
• The scaling factor $\frac{1}{\sqrt{d_k}}$ prevents the dot products from growing too large (pushing the softmax function into regions where it has extremely small gradients)

What exactly is $Q$, $K$ and $V$?:

• Empirically, Each token: asks a question (Q), compares it to all keys (K), and gathers a weighted mix of relevant values (V). Put it in another way, Q encodes what information the token needs, K encodes the what kind of information the token offers and V encodes the actual information to pass along
• $Q$, $K$, $V$ all come from the same sequence
• $QK^T$ measures how well each query matches each key and produces a $n \times n$ matrix
• $\text{softmax}$ converts similarities into attention weights with each row summing to 1
• finally, the output is a mixture of values, weighted by relevance ($\text{weights}$ x $V$)

Multi-Head Attention

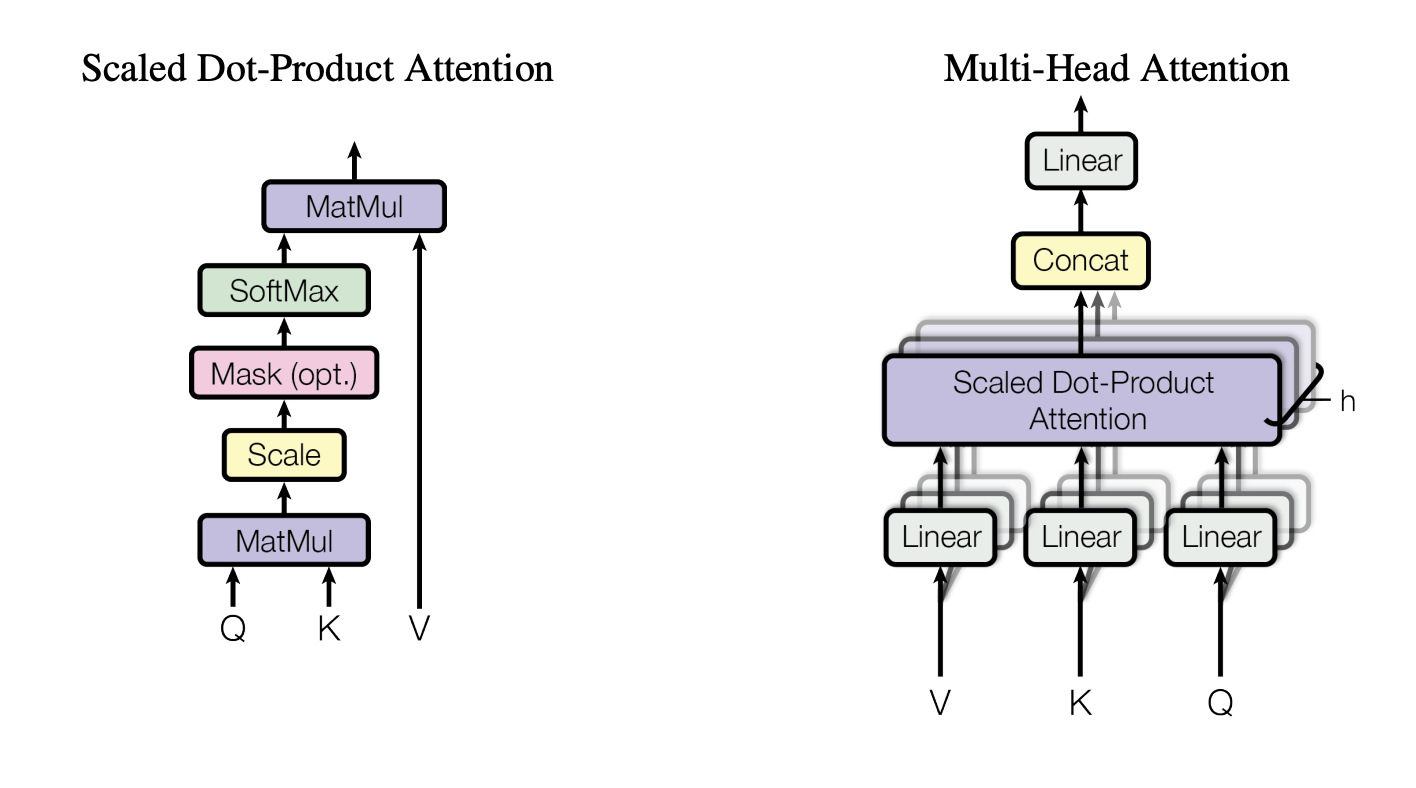
Instead of performing a single attention function, multi-head attention projects the queries, keys, and values $h$ times with different learned projections:

$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O$

Where each head is:

$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$

The key intuition here is that each head learns a different representation subspace and a different notion of relevance. Think of each head asking a different question and each head is running in parallel (not sequentially). Some heads can focus on grammar, vocab, object relations while others on delimeter tokens, coreference, quotation boundaries etc. Hence, more information can be captured within the same time with multiple heads working in parallel.

Question: Why not increase ${d_k}$ (make one head bigger) instead of using multiple heads?

(a) Softmax bottleneck

• One head → one softmax distribution
• Multiple heads → multiple independent distributions
• You get multiple sparse focus patterns, not one dense one

(b) Subspace specialization

• Each head projects inputs into a different learned subspace
• One large projection tends to entangle features
• Multiple smaller projections encourage disentanglement

(c) Non‑linearity through structure

• Even though attention is linear in V, multiple heads + concatenation increases expressivity
• Similar effect to having multiple convolution filters

(d) Multi‑head attention increases bandwidth and avoids information loss casued by early averaging:

• One head: one weighted sum per token
• h heads: h different summaries per token
• Final projection recombines them flexibly

Question: Why heads are smaller (${d_k} = \frac{d_{model}}{h}$)?

If we kept full dimensionality per head:

• Computation and memory would explode
• Heads would become redundant

By shrinking each head:

• Total cost stays roughly constant
• Each head is forced to specialize

Position Embeddings

Since the model has no recurrence nor convolution, in order for the model to make use of the order of the sequence, positional information is injected to the input embeddings using:

$PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d}}\right)$

$PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d}}\right)$

Acknowledgements

All images are taken from the research paper

Additional resources

• how transformers work